Đề kiểm tra 45 phút học kỳ I Toán 6, Chương I: Ôn tập và bổ túc về số tự nhiên (Đề 12)
Giải Sách
2020-05-09T10:23:37-04:00
2020-05-09T10:23:37-04:00
https://ibaihochay.site/index.php/toan-hoc-6/de-kiem-tra-45-phut-hoc-ky-i-toan-6-chuong-i-on-tap-va-bo-tuc-ve-so-tu-nhien-de-12-4907.html
https://ibaihochay.site/uploads/news/2020_04/de-kiem-tra-toan-6.jpg
Bài học hay
https://ibaihochay.site/uploads/bai-hoc-hay-logo.png
Thứ bảy - 09/05/2020 10:19
Đề kiểm tra 45 phút học kỳ I Toán 6, Chương I: Ôn tập và bổ túc về số tự nhiên, Có hướng dẫn giải
Bài 1. (2 điểm) Cho A = 963 + 2493 + 351 + x với x ∈ N. Tìm điều kiện của x để A chia hết cho 9, để A không chia hết cho 9.
Bài 2. (2 điểm) Tìm các chữ số a, b để số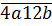 
chia hết cho cá 2 ; 5 và 9.
Bài 3. (3 điểm)
a) Tìm ƯCLN(36, 60), BCNN(36, 60)
b) So sánh tích của ƯCLN và BCNN của 36 và 60 với tích 36.60. Rút ra nhận xét gì ?
Bài 4. (2 điểm) Số học sinh khối 6 của một trường trong khoảng từ 200 đến 400, khi xếp hàng với mỗi hàng gồm 12, 15 hay 18 người thì đều thừa 3 học sinh. Tính số học sinh của khối 6 đó.
Bài 5. (7 điểm) Chứng minh rằng (n + 2010)(n + 2013) là một số chẵn, với mọi số tự nhiên n.
HƯỚNG DẪN GIẢI
Bài 1. Nếu x ⋮
9 thì A ⋮
9
Nếu x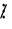 
9 thì A 
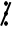9
Bài 2.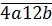 
⋮ 5 => b ∈ {0; 5}
Mà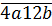 
⋮ 2 nên b = 0
Ta có số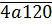 
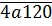⋮9 => 4 + a + 1 + 2 + 0 = 7 + a ⋮9
=> a = 2
Bài 3. a) ƯCLN(36, 60) = 12, BCNN(36, 60) = 180
b) ƯCLN(36, 60).BCNN(36, 60) = 2160 = 36.60
Rút ra nhận xét :
Với a, b e N* thì ƯCLN(a, b).BCNN(a, b) = a.b
Bài 4. Gọi số học sinh khối 6 của trường đó là x (200 ≤ x ≤ 400)
Ta có x - 3 là bội chung của 12 ; 15 ; 18 và 197 < x - 3 < 397.
BCNN(12, 15, 18) = 180
=> BC(12, 15, 18) = B(180) = {0 ; 180 ; 360 ; 540 ; ...}
Do đó x - 3 = 360
x = 363
Vậy số học sinh khối 6 của trường đó có 363 học sinh.
Bài 5. Nếu n là số chẵn thì n + 2010 là số chẵn
=> (n + 2010)(n + 2013) là số chẵn
• Nếu n là số lẻ thì n + 2013 là số chẵn => (n + 2013) là số chẵn
Vậy (n + 2010)(n + 2013) là số chẵn, với mọi số tự nhiên n.