Bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
Trả lời câu hỏi Toán 6 Tập 1 Bài 14 trang 46: Trong các số 7, 8, 9, số nào là số nguyên tố, số nào là hợp số ? Vì sao ?
Lời giải
- Số 7 là số nguyên tố vì 7 là số tự nhiên lớn hơn 1 và có hai ước là 1 và chính nó
- Số 8 là hợp số vì 8 là số tự nhiên lớn hơn 1 và có nhiều hơn hai ước đó là 1; 2; 4; 8
- Số 9 là hợp số vì 9 là số tự nhiên lớn hơn 1 và có nhiều hai ước là 1; 3; 9
Bài 115 (trang 47 sgk Toán 6 Tập 1): Các số sau là số nguyên tố hay hợp số?
312; 213; 435; 417; 3311; 67
Lời giải:
*Phương pháp kiểm tra một số a là số nguyên tố: Chia lần lượt a cho các số nguyên tố (2; 3; 5; 7; 11; 13; …) mà bình phương không vượt quá a
– 312 chia hết cho 2 nên không phải số nguyên tố.
– 213 có 2 + 1 + 3 = 6 nên chia hết cho 3. Do đó 213 không phải số nguyên tố.
– 435 chia hết cho 5 nên không phải số nguyên tố.
– 3311 chia hết cho 11 nên không phải số nguyên tố.
– 67 không chia hết cho 2; 3; 5; 7 nên 67 là số nguyên tố. (chỉ chia đến 7 vì các số nguyên tố khác lớn hơn 7 thì bình phương của chúng lớn hơn 67).
Kiến thức áp dụng
– Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
– Phương pháp kiểm tra số nguyên tố: Để kiểm tra số tự nhiên a (a > 1) có phải số nguyên tố hay không, ta chia a cho tất cả các số nguyên tố mà bình phương không vượt quá a.
Nếu a chia hết cho một số nguyên tố nào đó thì a là hợp số.
Nếu a không chia hết cho mọi số nguyên tố đó thì a là số nguyên tố.
Bài 116 (trang 47 sgk Toán 6 Tập 1): Gọi P là tập hơp các số nguyên tố. Điền kí hiệu ∈ , ∉ hoặc ⊂ vào ô trống cho đúng:
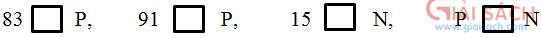
Lời giải:
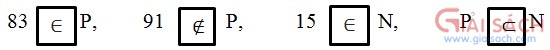
Ta có:
83 không chia hết cho 2; 3; 5; 7 nên 83 là số nguyên tố. Do đó 83 ∈ P.
91 chia hết cho 7 nên 91 không phải số nguyên tố. Do đó 91 ∉ P.
15 là số tự nhiên nên 15 ∈ N.
Các số nguyên tố đều là số tự nhiên nên P ⊂ N.
Kiến thức áp dụng
– P là tập hợp số nguyên tố. Số nguyên tố là số tự nhiên lớn hơn 1 chỉ có 2 ước là 1 và chính nó.
– Cách kiểm tra số nguyên tố: Chia số đó cho lần lượt các số nguyên tố 2; 3; 5; 7; 11; …. .
– Các kí hiệu:
∈ (thuộc): a ∈ A nếu a là phần tử của tập hợp A.
∉ (không thuộc): a ∉ A nếu a không phải phần tử của tập hợp A.
A ⊂ B (A là tập con của B) nếu mọi phần tử của A đều là phần tử của tập B.
Bài 117 (trang 47 sgk Toán 6 Tập 1): Dùng bảng nguyên tố ở cuối sách tìm các số nguyên tố trong các số sau:
117; 131; 313; 469; 647
Lời giải:
Tra bảng số nguyên tố trang 128 SGK Toán 6 tập 1, ta được:
- Các số 131; 313; 647 là số nguyên tố.
Bài 118 (trang 47 sgk Toán 6 Tập 1): Tổng (hiệu) sau là số nguyên tố hay hợp số?
a) 3.4.5 + 6.7 ; b) 7.9.11.13 - 2.3.4.7
c) 3.5.7 + 11.13.17 ; d) 16 354 + 67 541
Lời giải:
a) Ta có : (3.4.5) ⋮ 2 (vì 3.4.5 = 3.2.2.5 chia hết cho 2).
6.7 ⋮ 2 (vì 6.7 = 2.3.7 chia hết cho 2).
Do đó 3.4.5 + 6.7 ⋮ 2 nên 3.4.5 + 6.7 là hợp số.
b) 7.9.11.13 ⋮ 7 và 2.3.4.7 ⋮ 7 ⇒ (7.9.11.13 – 2.3.4.7) ⋮ 7.
Vậy (7.9.11.13 – 2.3.4.7) là hợp số.
c) 3.5.7 + 11.13.17 = 2536 ⋮ 2 nên 2536 là hợp số hay 3.5.7 + 11.13.17 là hợp số.
d) 16354 + 67541 = 83895 tận cùng bằng 5 nên chia hết cho 5. Do đó 16354 + 67541 là hợp số.
Bài 119(trang 47 sgk Toán 6 Tập 1): Thay chữ số vào dấu * để được hợp số:  ;
; 
Lời giải:
Tra bảng các số nguyên tố ta có 11, 13, 17, 19, 31, 37 là các số nguyên tố.
– Các hợp số có dạng 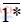 là 10 ; 12 ; 14 ; 15 ; 16 ; 18.
là 10 ; 12 ; 14 ; 15 ; 16 ; 18.
– Các hợp số có dạng 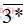 là: 30; 32; 33 ; 34 ; 35 ; 36 ; 38 ; 39.
là: 30; 32; 33 ; 34 ; 35 ; 36 ; 38 ; 39.
<<XEM MỤC LỤC