Bài 8: Chia hai lũy thừa cùng cơ số
Trả lời câu hỏi Toán 6 Tập 1 Bài 8 trang 29: Ta đã biết 53 . 54 = 57. Hãy suy ra:
57 : 53 = ?; 57 : 54 = ?
Lời giải
Ta có:
57 : 53 = 54
57 : 54 = 53
Trả lời câu hỏi Toán 6 Tập 1 Bài 8 trang 30: Viết thương của hai lũy thừa sau dưới dạng một lũy thừa:
a) 712 : 74;
b) x6 : x3 ( x ≠ 0)
c) a4 : a4 (a ≠ 0).
Lời giải
Ta có:
a) 712 : 74 = 7(12-4) = 78
b) x6 : x3 = x(6-3) = x3
c) a4 : a4 = a(4-4) = a0
Trả lời câu hỏi Toán 6 Tập 1 Bài 8 trang 30: Viết các số 538; abcd dưới dạng tổng các lũy thừa của 10.
Lời giải
538 = 5 . 100 + 3 . 10 + 8 = 5 . 102 + 3 . 101 + 8 . 100
(abcd) = a . 1000 + b . 100 + c . 10 + d = a . 103 + b . 102 + c . 101 + d . 100
Bài 67 (trang 30 sgk Toán 6 Tập 1): Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:
a) 38:34 b) 108:102 c) a6:a (a khác 0)
Lời giải
a) 38:34 = 38-4 = 34
b) 108:102 = 108-2 = 106
c) Lưu ý: a = a1
a6:a = a6-1 = a5
Kiến thức áp dụng
am : an = am-n (a ≠ 0; m ≥ n)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.
Bài 69 (trang 30 sgk Toán 6 Tập 1): Điền chữ Đ (đúng ) hoặc chứ S (sai) vào ô vuông:
a) 33 . 34 bằng: 312☐ 912☐ 37☐ 67☐
b) 55 : 5 bằng: 55☐ 54☐ 53☐ 14☐
c) 23 . 42 bằng: 86☐ 65☐ 27☐ 26☐
Lời giải
a) 33 . 34 = 33 + 4 = 37.
b) 55 : 5 = 55 – 1 = 54.
c) 23 . 42 = 8 . 16 = 23 . 24 = 23 + 4 = 27.
Vậy ta điền vào các ô trống như sau:
a) 33 . 34 bằng:

b) 55 : 5 bằng:

c) 23 . 42 bằng:

Kiến thức áp dụng
am . an = am+n; am : an = am – n (m ≥ n, a > 0).
Bài 70 (trang 30 sgk Toán 6 Tập 1): Viết các số: 987; 2564; 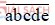 dưới dạng tổng các lũy thừa của 10.
dưới dạng tổng các lũy thừa của 10.
Lời giải
987 = 900 + 80 + 7
= 9.100 + 8.10 + 7
= 9.102 + 8.101 + 7.100
2564 = 2000 + 500 + 60 + 4
= 2.1000 + 5.100 + 6.10 + 4
= 2.103 + 5.102 + 6.101 + 4.100
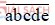 = a.10000 + b.1000 + c.100 + d.10 + e
= a.10000 + b.1000 + c.100 + d.10 + e
= a.104 + b.103 + c.102 + d.101 + e.100
Bài 71 (trang 30 sgk Toán 6 Tập 1): Tìm số tự nhiên c biết rằng với mọi n ∈ N* ta có:
a) cn = 1; b) cn = 0.
Lời giải
Với mọi n ∈ N* thì:
a) cn = 1 suy ra c = 1
b) cn = 0 suy ra c = 0
Ghi nhớ: 1n = 1 và 0n = 0
Tập N* là các số tự nhiên khác 0. Nếu n ∈ N thì khi đó n có thể bằng 0 và câu a) sẽ cho kết quả khác. Cụ thể là: c0 = 1 suy ra c ∈ N.
Bài 72 (trang 31 sgk Toán 6 Tập 1): Số chính phương là số bằng bình phương của một số tự nhiên (ví dụ 0, 1, 4, 9, 16, ...). Mỗi tổng sau có là một số chính phương không?
a) 13 + 23
b) 13 + 23 + 33
c) 13 + 23 + 33 + 43
Lời giải
(SCP là viết tắt của số chính phương)
Ta có: 13 = 1; 23 = 8; 33 = 27; 43 = 64.
● 13 + 23 = 1 + 8 = 9.
Mà 9 = 32 là SCP (vì là bình phương của 3) nên 13 + 23 là SCP.
● 13 + 23 + 33 = 1 + 8 + 27 = 36.
Mà 36 = 62 là SCP (vì là bình phương của 6) nên 13 + 23 + 33 là SCP.
● 13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100.
Mà 100 = 102 là SCP (vì là bình phương của 10) nên 13 + 23 + 33 + 43 là SCP.
Vậy mỗi tổng đã cho đều là số chính phương.
Kiến thức áp dụng
+ Các bạn cần nhớ lại các kết quả của bài tập 58 và 59 để làm bài tập này.
(các kết quả này đã dặn các bạn cần nhớ thật kĩ, học thuộc lòng)
Cụ thể: 13 = 1; 23 = 8; 33 = 27; 43 = 64; …
12 = 1; 22 = 4; 32 = 9; 42 = 16; 52 = 25; 62 = 36; 72 = 49; 82 = 64; 92 = 81; …
+ Các bạn cần nhớ thêm một khái niệm số nữa: số chính phương là số bằng bình phương của một số tự nhiên.
20 số chính phương đầu tiên: 0; 1; 4; 9; 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196; 225; 256; 289; 324; 361; 400.
* Mở rộng:
Các bạn có thể để ý thấy rằng 3 = 1 + 2; 6 = 1 + 2 + 3; 10 = 1 + 2 + 3 + 4.
Ta viết lại như sau:
13 + 23 = (1 + 2)2 ;
13 + 23 + 33 = (1 + 2 + 3)2 ;
13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2.
Theo quy luật đó ta có thể tính nhanh tổng của dãy lập phương :
13 + 23 + 33 + 43 + 53 = (1 + 2 + 3 + 4 + 5)2 ;
13 + 23 + 33 + 43 + 53 + 63 = (1 + 2 + 3 + 4 + 5 + 6)2 ;
…
Tổng quát : Với mọi số tự nhiên n ta luôn có :
13 + 23 + 33 +…+ n3 = (1 + 2 + 3 +…+ n)2.
Kết quả tổng quát trên đều đã được chứng minh ở các lớp cao hơn.
Các bạn có thể kiểm tra một vài công thức đầu bằng cách tính toán như trên.
<<XEM MỤC LỤC