Bài 9: Quy tắc chuyển vế
Luyện tập (Trang 87-88)
Bài 66 (trang 87 SGK Toán 6 Tập 1): Tìm số nguyên x, biết 4 – (27 - 3) = x – (13 - 4).
Lời giải
4 – (27 – 3) = x – (13 – 4)
4 – 27 + 3 = x – 13 + 4 (bỏ ngoặc)
4 – 27 + 3 + 13 – 4 = x (chuyển vế –13 và 4)
–27 + 16 = x
–11 = x.
Vậy x = –11.
Bài 67 (trang 87 SGK Toán 6 Tập 1): Tính:
a) (-37) + (-112)
b) (-42) + 52
c) 13 - 31
d) 14 - 24 - 12
e) (-25) + 30 - 15
Lời giải
a) (–37 ) + (–112)
= –(37 + 112) (cộng hai số nguyên âm).
= –149.
b) (–42) + 52
= 52 – 42 (cộng hai số nguyên khác dấu)
= 10
c) 13 – 31 = –31 + 13 = – (31 – 13) = –18.
d) 14 – 24 – 12 = 14 – (24 + 12) = 14 – 36 = – (36 – 14) = –22.
e) (–25) + 30 – 15 = 30 – 25 – 15 = 30 – (25 + 15) = 30 – 40 = –10
Bài 68 (trang 87 SGK Toán 6 Tập 1): Một đội bóng đá năm ngoái ghi được 27 bàn và để thủng lưới 48 bàn. Năm nay đội bóng ghi được 39 bàn và để thủng lưới 24 bàn. Tính hiệu số bàn thắng – thua của đội bóng đó trong mỗi mùa giải.
Lời giải
+ Năm ngoái :
Bàn thắng : 27 bàn
Bàn thua : 48 bàn
Hiệu số bàn thắng – thua : 27 – 48 = –48 + 27 = –(48 – 27) = –21 (bàn)
+ Năm nay :
Bàn thắng : 39 bàn
Bàn thua : 24 bàn.
Hiệu số bàn thắng – thua : 39 – 24 = 15 (bàn).
Bài 69 (trang 87 SGK Toán 6 Tập 1): Trong bảng dưới đây có nhiệt độ cao nhất và nhiệt độ thấp nhất của một số thành phố vào một ngày nào đó. Hãy ghi vào cột bên phải số độ chênh lệch (nhiệt độ cao nhất trừ nhiệt độ thấp nhất) trong ngày đó của một thành phố.
| Thành phố | Nhiệt độ cao nhất | Nhiệt độ thấp nhất | Chênh lệch nhiệt độ |
| Hà Nội | 25ºC | 16ºC | |
| Bắc Kinh | –2ºC | –16ºC | |
| Mat–xcơ–va | –2ºC | –16ºC | |
| Pa–ri | 12ºC | 2ºC | |
| Tô–ky–ô | 8ºC | –4ºC | |
| Tô–rôn–tô | 2ºC | –5ºC | |
| Niu–yooc | 12ºC | –1ºC | |
Lời giải
| Thành phố | Nhiệt độ cao nhất | Nhiệt độ thấp nhất | Chênh lệch nhiệt độ |
| Hà Nội | 25ºC | 16ºC | 9ºC |
| Bắc Kinh | –2ºC | –16ºC | 6ºC |
| Mat–xcơ–va | –2ºC | –16ºC | 14ºC |
| Pa–ri | 12ºC | 2ºC | 10ºC |
| Tô–ky–ô | 8ºC | –4ºC | 12ºC |
| Tô–rôn–tô | 2ºC | –5ºC | 7ºC |
| Niu–yooc | 12ºC | –1ºC | 13ºC |
* Cụ thể:
+ Hà Nội: 25 – 16 = 9
+ Bắc Kinh: (–1) – (–7) = –1 + 7 = 6.
+ Mát– xcơ–va: (–2) – (–16) = –2 + 16 = 14.
+ Pa–ri: 12 – 2 = 10
+ Tô–ky–ô: 8 – (–4) = 8 + 4 = 12.
+ Tô–rôn–tô: 2 – (–5) = 2 + 5 = 7
+ Niu–yooc: 12 – (–1) = 12 + 1 = 13.
Bài 70 (trang 88 SGK Toán 6 Tập 1): Tính các tổng sau một cách hợp lý:
a) 3784 + 23 – 3785 – 15
b) 21 + 22 + 23 + 24 – 11 - 12 - 13 - 14
Lời giải
a) 3784 + 23 – 3785 – 15
= (3784 – 3785) + (23 – 15)
= (–1) + 8
= –7
b) 21 + 22 + 23 + 24 – 11 – 12 – 13 – 14
= (21 – 11) + (22 – 12) + (23 – 13) + (24 – 14)
= 10 + 10 + 10 + 10
= 40.
Bài 71 (trang 88 SGK Toán 6 Tập 1): Tính nhanh:
a) -2001 + (1999 + 2001)
b) (43 - 863) - (137 - 57)
Lời giải
a) –2001 + (1999 + 2001)
= –2001 + 1999 + 2001
= 2001 – 2001 + 1999 = 1999.
b) (43 – 863) – (137 – 57)
= 43 – 863 – 137 + 57
= (43 + 57) – (863 + 137)
= 100 – 1000
= –900
Bài 72 (trang 88 SGK Toán 6 Tập 1): Đố: Cho chín tấm bìa có ghi số và chia thành ba nhóm như hình 51. Hãy chuyển một tấm bìa từ nhóm này sang nhóm khác sao cho tổng các số trong mỗi nhóm đều bằng nhau.
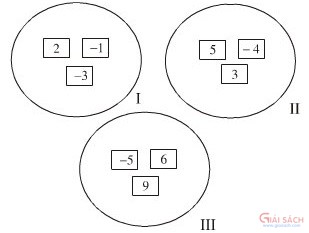
Hình 51
Lời giải
Tổng tất cả các số trong cả 3 nhóm là :
2 + (–1) + (–3) + 5 + 3 + (–4) + (–5) + 6 + 9
= (2 + 6 + 9) + (–1) + (–4) + [5 + (–5)] + [3 + (–3)]
= 17 – 5 + 0 + 0 = 12.
Để tổng các số trong mỗi nhóm bằng nhau thì mỗi nhóm phải có tổng là 12 : 3 = 4
Mà:
Nhóm II có 5 + 3 + (–4) = 8 – 4 = 4 nên giữ nguyên
Nhóm III có 6 + 9 + (–5) = 10 nên cần bớt 6 để có tổng bằng 4.
Nhóm I có 2 + (–3) + (–1) = –2 nên cần thêm 6 để có tổng bằng 4.
Vậy ta cần chuyền bìa số 6 từ nhóm (III) sang nhóm I thì tổng mỗi nhóm đều bằng nhau và bằng 4.
<<XEM MỤC LỤC