Bài 12: Dấu hiệu chia hết cho 3, cho 9
Trả lời câu hỏi Toán 6 Tập 1 Bài 12 trang 40: Trong các số sau, số nào chia hết cho 9, số nào không chia hết cho 9: 621; 1205; 1327; 6354
Lời giải
- Các số chia hết cho 9 là 621 và 6354 vì số 621 có tổng các chữ số là 6 + 2 + 1 = 9 chia hết cho 9 và số 6354 có tổng các chữ số là 6 + 3 + 5 + 4 = 18 chia hết cho 9
- Các số không chia hết cho 9 là 1205 và 1327 vì số 1205 có tổng các chữ số là 1 + 2 + 0 + 5 = 8 không chia hết cho 9 và số 1327 có tổng cá chữ số là 1 + 3 + 2 + 7 = 13 không chia hết cho 9
Trả lời câu hỏi Toán 6 Tập 1 Bài 12 trang 41: Điền chữ số vào dấu * để được số (157*) chia hết cho 3.
Lời giải
(157*) ⋮ 3 khi ( 1 + 5 + 7 + * ) ⋮ 3 ⇒ (13 + * ) ⋮ 3
Suy ra * = 2 hoặc * = 5 hoặc * = 8 ( vì * là số tự nhiên và * < 10)
Vậy chữ số thay cho * là 2 hoặc 5 hoặc 8
Bài 101 (trang 41 sgk Toán 6 Tập 1): Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?
187; 1347; 2515; 6534; 93258
Lời giải:
Ta có: 1 + 8 + 7 = 16 không chia hết cho 3 và 9
1 + 3 + 4 + 7 = 15 chia hết cho 3, không chia hết cho 9
2 + 5 + 1 + 5 = 13 không chia hết cho 3 và 9
6 + 5 + 3 + 4 = 18 chia hết cho 3 và 9.
9 + 3 + 2 + 5 + 8 = 27 chia hết cho 3 và 9.
Theo tính chất chia hết cho 3 và 9 ta có:
– Các số chia hết cho 3 gồm: 1347; 6534; 93258.
– Các số chia hết cho 9 gồm: 6534; 93258.
Kiến thức áp dụng
– Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
– Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Bài 102 (trang 41 sgk Toán 6 Tập 1): Cho các số 3564; 4352; 6531; 6570; 1248
a) Viết tập hơp A các số chia hết cho 3 trong các số trên.
b) Viết tập hợp B các số chia hết cho 9 trong các số trên.
c) Dùng kí hiệu ⊂ để thể hiện quan hệ giữa hai tập hợp trên.
Lời giải:
Ta có: 3 + 5 + 6 + 4 = 18 chia hết cho 3 và 9.
4 + 3 + 5 + 2 = 14 không chia hết cho 3 và 9.
6 + 5 + 3 + 1 = 15 chia hết cho 3 nhưng không chia hết cho 9.
6 + 5 + 7 + 0 = 18 chia hết cho 3 và 9.
1 + 2 + 4 + 8 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
a) Tập hợp các số chia hết cho 3 là A = {3564; 6531; 6570; 1248}
b) Tập hợp các số chia hết cho 9 là B = {3564; 6570}.
c) Vì mỗi phần tử của tập B đều là phần tử của tập A nên B ⊂ A.
Bài 103 (trang 41 sgk Toán 6 Tập 1): Tổng (hiệu) sau có chia hết cho 3 không, có chia hết cho 9 không?
a) 1251 + 5316 ;
b) 5436 - 1324 ;
c) 1.2.3.4.5.6 + 27
Lời giải:
a) 1 + 2 + 5 +1 = 9 chia hết cho 3 và 9.
5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
1251 ⋮ 3 và 5316 ⋮ 3 ⇒ 1251 + 5316 ⋮ 3.
1251 ⋮ 9 và 5316 ⋮̸ 9 nên 1251 + 5316 ⋮̸ 9.
b) 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
1 + 3 + 2 + 4 = 10 không chia hết cho cả 3 và 9.
Do đó:
5436 ⋮ 3 và 1324 ⋮̸ 3 nên 5436 – 1324 ⋮̸ 3.
5436 ⋮ 9 và 1324 ⋮̸ 9 nên 5436 – 1324 ⋮̸ 9.
c) Ta có: 1.2.3.4.5.6 chia hết cho 3.
1.2.3.4.5.6 = 1.2.4.5.(3.6) = 1.2.4.5.18 = 1.2.4.5.2.9 chia hết cho 9.
27 chia hết cho 3 và 9.
Do đó 1.2.3.4.5.6 + 27 chia hết cho 3 và 9.
Bài 104 (trang 42 sgk Toán 6 Tập 1): Điền chữ số vào dấu * để:
a)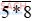 
chia hết cho 3;
b)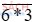 
chia hết cho 9;
c)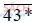 
chia hết cho cả 3 và 5;
d)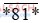 
chia hết cho cả 2 ,3, 5, 9 ( trong một số có nhiều dấu * , các dấu * không nhất thiết thay bởi các chữ số giống nhau)
Lời giải:
a) Ta có: 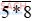⋮ 3 chỉ khi (5 + * + 8) ⋮ 3 hay (13 + *) ⋮ 3.
Mà 0 ≤ * ≤ 9 nên * = 2; 5 hoặc 8.
Vậy các số 528; 558; 588 ⋮ 3.
b) ⋮ 9 chỉ khi (6 + * + 3) ⋮ 9 hay (9 + *) ⋮ 9.
Mà 0 ≤ * ≤ 9 nên * = 0 hoặc 9.
Vậy các số 603; 693 ⋮ 9.
c) 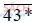chia hết cho 5 chỉ khi * = 0 hoặc 5.
* = 0 thì 4 + 3 + 0 = 7 ⋮̸ 3 nên 430 ⋮̸ 3 (loại).
* = 5 thì 4 + 3 + 5 = 12 ⋮ 3 nên 435 ⋮ 3 (thỏa mãn).
Vậy 435 chia hết cho cả 3 và 5.
d) 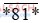chia hết cho 2 và 5 nên chữ số tận cùng phải bằng 0.
Do đó số cần tìm có dạng .
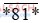chia hết cho 3 và 9 chỉ khi (* + 8 + 1 + 0) ⋮ 9 (vì chia hết cho 9 thì chia hết cho 3) hay (* + 9) ⋮ 9.
Mà 0 < * < 10 nên * = 9.
Vậy số chia hết cho cả 2, 3, 5, 9 là 9810.
Bài 105 (trang 42 sgk Toán 6 Tập 1): Dùng ba trong bốn chữ số 4, 5, 3, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó:
a) Chia hết cho 9
b) Chia hết cho 3 và không chia hết cho 9
Lời giải:
a) Bộ ba số có tổng chia hết cho 9 là (4; 5; 0) (4 + 5 + 0 = 9)
Do đó các số được lập từ ba số trên cũng chia hết cho 9 .
Ta lập được các số là 450; 405; 540; 504.
b) Bộ ba số có tổng chia hết cho 3 nhưng không chia hết cho 9 là (4 ; 5 ; 3)
(4 + 5 + 3 = 12 chia hết cho 3 nhưng không chia hết cho 9).
Do đó các số được lập từ ba số trên cũng chia hết cho 3 nhưng không chia hết cho 9.
Ta lập được các số: 453; 435; 543; 534; 345; 354.
<<XEM MỤC LỤC